Ölbaum’s Delirium

So I’ve received this e-mail (in French) a couple of times, titled Two Moons in the Sky, saying that on August 27th this year (though the two times I received it were on different years) at 00:30 (precisely, mind you, not during the whole night or for a few nights before and after that date), Mars will be the brightest object in the night sky, as bright (sometimes also as big) as the full Moon, even though it’s 55 million kilometers from Earth, and that it won’t happen again before year 2287!

I mean, WOW!

No, not World of Warcraft. No, not “Wow, Mars will be as bright as the full Moon” either.

Rather, “Wow, I have friends who believe this shit, who believe it enough to forward it to me as a fact, not even to ask me if it’s true.” (I happen to have a teeny, tiny PhD in some branch of Physics. Not many people know that.)

What’s good with this joke is that, by a happy coincidence on the numbers involved, the calculations needed to debunk it can be done in your head. Well, maybe not in your head, but certainly in mine.

See, everybody knows that the Earth is 150 million kilometers away from the Sun. The e-mail tells us the Earth-Mars distance at its shortest will be 55 million kilometers, which happens to be the only correct information in the whole message. This gives us the Sun-Mars distance as 150 + 55 = 205, make is 200 million kilometers.

Now the amount of sunlight received by a celestial object (or any kind of object, really) is inversely proportional to the square of its distance to the Sun, meaning that if you double the distance, it receives four times less light. So the amount of light received by Mars compared to the Moon (which is at the same distance from the Sun than the Earth) is

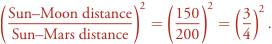
Let’s keep it this way for now.

Then the amount of light reflected by the planet is proportional to its surface, which is proportional to the square of its diameter. Maybe not everybody knows that Mars (6772 kilometers in diameter) is twice as big as the Moon (3475 kilometers, I told you the numbers involved were convenient), but people know that Mars is “a bit like Earth”, which would make it four times bigger than the Moon, which would be in the benefit of Mars and still work. But let’s stick with the correct numbers. The amount of light reflected by Mars compared to the Moon is therefore

Finally, the amount of light received by the Earth from each of our objects is, like before, inversely proportional to the square of the distance. Again, everybody knows that the Moon is 384 thousand kilometers away from the Earth. That’s the average distance. The maximum distance is rather 406 thousand kilometers. I’ll round it to 440 thousand kilometers because it’s in the detriment of the Moon and it’s convenient. So the amount of light received by the Earth from Mars compared to the Moon would be (beware the units)

Now it might be that the surface of Mars reflects light better than the surface of the Moon. It’s even probable: Mars is red whereas the Moon is black (Don’t believe me? Remember those rocks they took back from there, like exactly forty years ago? Did they look bright white?). But I’ll assume they both reflect light equally so we can compare the numbers with real data in the end. We can make the calculation again with Mars ten times brighter than the Moon later if you want.

So, to sum up, we have:

• Amount of light received by Mars compared to the Moon: (3/4)²;
• Amount of light reflected by Mars compared to the Moon: 2²;
• Amount of light received by the Earth from Mars compared to the Moon: (8/1000)².

Let’s multiply all this (because the light reflected is proportional to the light received from the Sun, and the light received on Earth is proportional to the light reflected):

The light we get from Mars, in the best case ever, is almost seven thousand times less than the light we get from the full Moon. What a surprise! And if we had taken Mars to be as big as the Earth (four times bigger than the Moon instead of two, gives another factor 4 once squared) and ten times brighter than the Moon (i.e. very wrong numbers in its favour), it would still appear 170 times fainter.

Now let’s check this result quickly. The Wikipedia article on apparent magnitude tells us that the magnitude of the full Moon is -12.6 and the maximum brightness of Mars is -2.9. It also tells us that the ratio in brightness between two objects is given by

where x is the difference between the two magnitudes. In our case:

We weren’t far with our seven thousand, given the approximations we made, don’t you reckon?

Do we need to check the claim that Mars can appear as big as the Moon, too? That won’t take long, now that we’re experts in the field. The apparent size of an object in the sky is given by the angle under which you see its diameter. In radians and for such small angles, it’s calculated as diameter/distance. Hey, we happen to have all the necessary data already. For Mars:

For the Moon:

That is, Mars appears 70 times smaller than the Moon in the sky.

So next time you see a message that claims such unbelievable things, make a quick mental calculation before forwarding it to everybody. Or even easier, ask yourself if you have ever seen a celestial object that looked bigger than a dot to the naked eye, apart from the Sun and Moon, and check on the Internet. There are sites like Hoax-Slayer (English) or HoaxBuster (French) dedicated to this and checking the validity of such e-mails can be done very quickly.

Next time in this column: why doesn’t the height at which you must throw a grenade to have it explode the moment it touches the ground depend on the weight of the grenade?